Big-O Notation
Categorizes algorithms on time/memory based on input.
Why?
- Helps us make decisions on what data structures and algorithms to use.
Fundamental concept
As input grows, how fast does computation or memory grow?
Important concepts
Growth is with respect to input
fn sum_char_codes(input: String) -> u32 {
let mut i = 0;
for char in input.chars() {
i += char as u32;
}
i
}
It runs an iteration in the for loop for the length of the string.
This function has
(Generally, look for loops to determine time complexity)
You always drop constants
While practically important, they're not theoretically important.
For example, if comparing
We're not concerned with the exact time, but instead, how it grows.
Practical and theoretical differences
Just because
Remember, we drop constants. Therefore,
For example, in sorting algorithms, we use insertion sort for small inputs. Though slower in the theoretical sense because it's
Consider the worst-case scenario
fn sum_char_codes(input: String) -> u32 {
let mut i = 0;
for char in input.chars() {
if char == 'E' { // checks if char is 'E', then instantly breaks
return i;
}
i += char as u32;
}
i
}
This function still has
While there are some algorithms where it's better to reason using the best case and the average case, most of the time, we're concerned with the worst-case scenario.
In interviews, almost always assume the worst-case scenario.
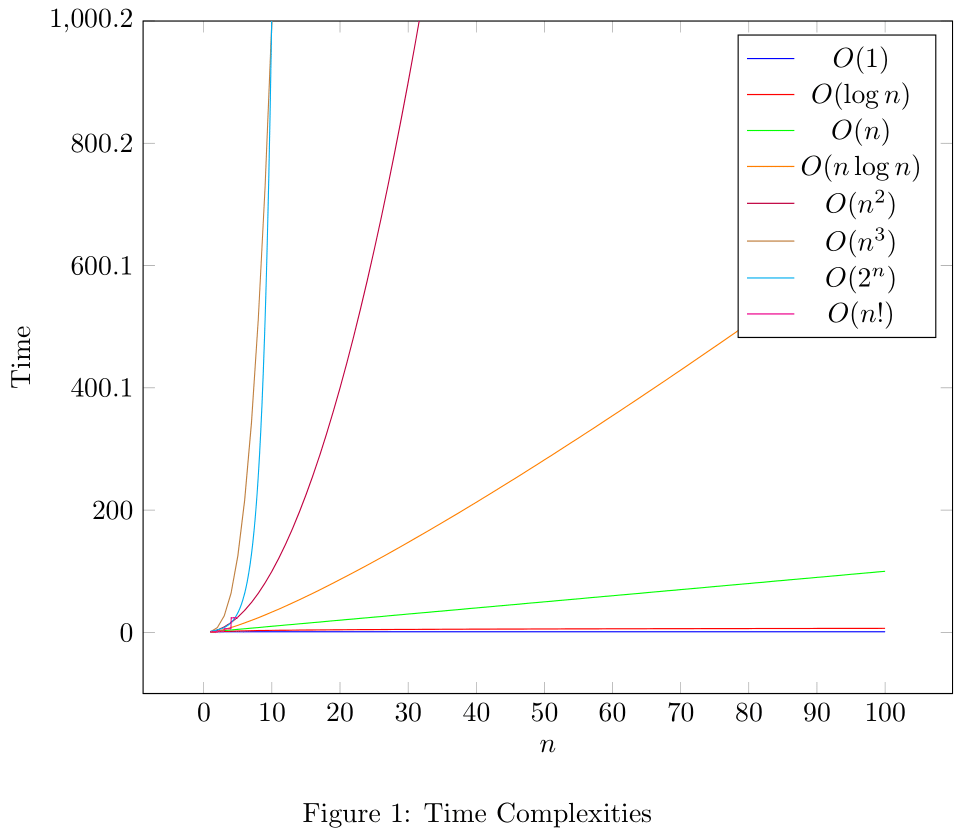
Common Big-O runtimes
| Big-O | Name | Example | Notes |
|---|---|---|---|
| Constant | Hash table lookup | Fastest | |
| Logarithmic | Binary search | Fast | |
| Linear | Simple search | Slow | |
| Log-linear | Quicksort | Fast | |
| Quadratic | Selection sort | Slow | |
| Cubic | Matrix multiplication | Slow | |
| Exponential | Traveling salesperson | Very slow | |
| Factorial | Traveling salesperson | Very slow |
Simple examples
fn sum_char_codes(input: String) -> u32 {
let mut i = 0;
for char in input.chars() { // loop 1
for char in input.chars() { // loop 2
i += char as u32;
}
}
i
}
For each character in the string, we iterate through the string again. This is
fn sum_char_codes(input: String) -> u32 {
let mut i = 0;
for char in input.chars() { // loop 1
for char in input.chars() { // loop 2
for char in input.chars() { // loop 3
i += char as u32;
}
}
}
i
}
Just like the previous example, but we iterate through the string three times. This is
(Quicksort) - will be covered in a later section.
Binary search trees.
This is a very unique time complexity.
Other notations
For example,
For example,
Space complexity
Space complexity is the amount of memory an algorithm takes up. Generally it's less consequential than time complexity.
return <Component {...props} /> // O(n) time and O(n) space
Conclusion
- Big-O is a way to categorize algorithms based on time/memory.
- Growth is with respect to input.
- You always drop constants.
- In most cases consider the worst-case scenario.